What’s inside KeLP

The KeLP framework is written in Java and it has been developed in different Maven packages according to a modularization aimed at logically separating the different components of the library. KeLP is currently composed of the following 4 packages:

  • kelp-core: it contains the infrastructure of abstract classes and interfaces to work with KeLP. Furthermore, some implementations of algorithms, kernels and representations are included, to provide a base operative environment.
  • kelp-additional-kernels: it contains several kernel functions that extend the set of kernels made available in the kelp-core project. Moreover, this project implements the specific representations required to enable the application of such kernels. In this project the following kernel functions are considered: Sequence kernels, Tree kernels and Graphs kernels.
  • kelp-additional-algorithms: it contains several learning algorithms extending the set of algorithms provided in the kelp-core project, e.g. the C-Support Vector Machine or ν-Support Vector Machine learning algorithms. In particular, advanced learning algorithms for classification and regression can be found in this package. The algorithms are grouped in: 1) Batch Learning, where the complete training dataset is supposed to be entirely available during the learning phase; 2) Online Learning, where individual examples are exploited one at a time to incrementally acquire the model.
  • kelp-full: this is the complete package of KeLP. It aggregates the previous modules in one jar. It contains also a set of fully functioning examples showing how to implement a learning system with KeLP. Batch learning algorithm as well as Online Learning algorithms usage is shown here. Different examples cover the usage of standard kernel, Tree Kernels and Sequence Kernel, with caching mechanisms.

A small tutorial for the import of packages via Maven can be found here.
In the following, a closer look at the main classes is provided.

Data

In many domains, data are naturally modeled with a structured representation, preserving its inherent form. Operating directly on structured representation can be then necessary or convenient in many circumstances. In the next paragraph we will introduce kernel methods which enable this opportunity providing an effective and elegant solution.

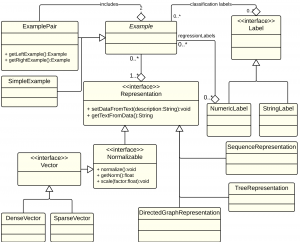
Our platform completely supports structured data allowing the possibility to define new representations or to exploit the already implemented ones. SimpleExample models the base form of an Example and consists of:

  • a set of Labels that can be used in various scenarios like (multi-label) classification or (multi-variate) regression;
  • a set of Representations which allows to model the same instance in different forms. For instance a sentence can be modeled into a Bag-of-Words feature vector and into a parse tree. Currently the platform implements DenseVector, SparseVector and TreeRepresentation.

Moreover the platform enables the definition of more complex example forms like ExamplePair which are commonly exploited in tasks like re-ranking as in Shen and Joshi (2003), entailment as in Zanzotto et al. (2009) or paraphrase detection as in Annesi et al. (2014).

Figure 1: class diagram of KeLP data

Kernels

In machine learning, kernel methods are a class of algorithms for pattern analysis, in which the objective is to find general types of relations in datasets. In particular, kernel methods leverage on the so called kernel functions, which enable them to operate in an implicit high-dimensional feature space without explicitly computing the coordinates of the data in that space. This operation is often cheaper from a computational perspective and it is called the kernel trick. Kernel functions have been introduced for sequence data, graphs, trees, text, images, as well as vectors. One of the most appealing characteristics of kernels is that they can be composed and combined in order to create richer similarity metrics in which different information from different Representations can be simultaneously exploited ((Shawe-Taylor and Cristianini, 2004a)).
As shown in the figure below, KeLP completely supports the composition and combination mechanisms providing three abstractions of the Kernel class:
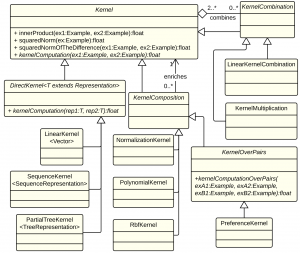
  • DirectKernel: in computing the kernel similarity it operates directly on a specific Representation that it automatically extract from the Examples to be compared. Currently KeLP implements LinearKernel over Vector representations, SubTreeKernel from (Collins and Duffy, 2001) and PartialTreeKernel from (Moschitti, 2006) over TreeRepresentations.
  • KernelComposition: it enriches the kernel similarity provided by any another Kernel. Currently KeLP implements PolynomialKernel, RBFKernel, NormalizationKernel and PreferenceKernel (introduced in Shen and Joshi (2003)).
  • KernelCombination: it combines different Kernels in a specific function. At the moment KeLP implements LinearKernelCombination which applies a weighted linear combination of Kernels

KeLP completely decouples kernels from algorithms so any Kernel implementation can be equipped in any kernelized algorithm: the learning algorithm employs the Kernel completely ignoring the specific operation it evaluates and the Representations it exploits.

Figure 2: class diagram of KeLP kernels

Machine Learning Algorithms

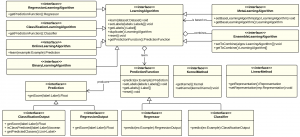
In Machine Learning a plethora of learning algorithms have been defined for different purposes and many variations of the existing ones as well as completely new learning methods are often proposed. Furthermore, learning algorithms can be composed and combined in ensemble methods, in meta learning algorithms like AdaBoost or in particular learning schemas like one-vs-all or one-vs-one. KeLP tries to formalize this large world proposing a comprehensive set of interfaces (see figure below) to support the implementation of new algorithms:

  • ClassificationLearningAlgorithm: for algorithms that learn from labelled data how to classify new instances. The current implementations include C-SVM, ν-SVM, one-class SVM (Chang and Lin, 2011) and Pegasos (Shalev-Shwartz et al., 2007).
  • OnlineLearningAlgorithm: it support the definition of online learning algorithms, like the Perceptron or the Passive Aggressive algorithms, (Crammer et al., 2006).
  • RegressionLearningAlgorithm: for algorithms that learn from labelled data a regression function. Currently KeLP implements ε-SVR (Chang and Lin, 2011), Linear and Kernelized Passive Aggressive Regression (Crammer et al., 2006).
  • ClusteringAlgorithm: for algorithms that are able to organize a dataset into clusters. Currently KeLP implements kernel-based clustering from Kulis et al. (2005).
  • MetaLearningAlgorithm: for learning approaches that rely on another algorithm. We implemented Multi-classification schemas, e.g. One-VS-One and One-VS-All as well as budgeted policies of online learning algorithms like Randomized Budget Perceptron (Cesa-Bianchi and Gentile (2006)) and Stoptron (discussed in Orabona et al. (2008)).
  • EnsembleLearningAlgorithm: for algorithms that combine other algorithms in order to provide a more robust solution.
  • BinaryLearningAlgorithm: this interface is implemented to derive binary classifiers. Notice that also One-Class classifier can extend this interface as they learn a binary classifier even being not provided of negative examples. Moreover, this interface can be used also to implement univariate regression algorithms, such as ε-SVR

Algorithms exploiting kernel functions must implement KernelMethod, while algorithms operating directly in an explicit feature space must implement LinearMethod. In KeLP algorithms are divided in two main entities: LearningAlgorithm and PredictionFunction. The former applies the learning process in order to properly set parameters that characterize the latter which is used to provide predictions on new data.

Figure 3: class diagram of KeLP algorithms

References

Paolo Annesi, Danilo Croce, and Roberto Basili. Semantic compositionality in tree kernels. In Proceedings of the 23rd ACM International Conference on Conference on In- formation and Knowledge Management, CIKM ’14, pages 1029–1038, New York, NY, USA, 2014. ACM.

Nicol Cesa-Bianchi and Claudio Gentile. Tracking the best hyperplane with a simple budget perceptron. In Proc. Of The Nineteenth Annual Conference On Computational Learning Theory, pages 483–498. Springer-Verlag, 2006.

Chih-Chung Chang and Chih-Jen Lin. LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology, 2:27:1–27:27, 2011.

Michael Collins and Nigel Duffy. Convolution kernels for natural language. In Proceedings of the 14th Conference on Neural Information Processing Systems, 2001.

Koby Crammer, Ofer Dekel, Joseph Keshet, Shai Shalev-Shwartz, and Yoram Singer. On-line passive-aggressive algorithms. Journal of Machine Learning Research, 7:551–585, December 2006. ISSN 1532-4435.

Danilo Croce, Alessandro Moschitti, and Roberto Basili. Structured lexical similarity via convolution kernels on dependency trees. In Proceedings of EMNLP, Edinburgh, Scotland, UK., 2011.

Brian Kulis, Sugato Basu, Inderjit Dhillon, and Raymond Mooney. Semi-supervised graph clustering: A kernel approach. In Proceedings of the ICML 2005, pages 457–464, New York, NY, USA, 2005. ACM.

Alessandro Moschitti. Efficient convolution kernels for dependency and constituent syntactic trees. In ECML, Berlin, Germany, September 2006.

Francesco Orabona, Joseph Keshet, and Barbara Caputo. The projectron: a bounded kernel-based perceptron. In Int. Conf. on Machine Learning, 0 2008. IDIAP-RR 08-30.

S. Shalev-Shwartz, Y. Singer, and N. Srebro. Pegasos: Primal estimated sub–gradient solver for SVM. In Proceedings of the International Conference on Machine Learning, 2007.

John Shawe-Taylor and Nello Cristianini. Kernel Methods for Pattern Analysis. Cambridge University Press, New York, NY, USA, 2004a. ISBN 0521813972.

Libin Shen and Aravind K. Joshi. An svm based voting algorithm with application to parse reranking. In In Proc. of CoNLL 2003, pages 9–16, 2003.

Yoram Singer and Nathan Srebro. Pegasos: Primal estimated sub-gradient solver for svm. In In ICML, pages 807–814, 2007.

Fabio massimo Zanzotto, Marco Pennacchiotti, and Alessandro Moschitti. A machine learning approach to textual entailment recognition. Nat. Lang. Eng., 15(4): 551–582, October 2009. ISSN 1351-3249.